chiral.grolim
Universal Kydex Sheath Extension
- Joined
- Dec 2, 2008
- Messages
- 6,422
...One of the main problems I've had is trying to conceptualize how a convex angle is measured. I never understood how a somewhat curved surface could be thought of, and measured, as an angle. Where on the curve is the "angle" supposed to be?
I think another problem in my understanding, which you mentioned in both posts 6 and 12, is regarding "equal edge angle". Often the diagrams and drawings of flat and convex edges do not appear to be scaled the same, with the convex appearing thicker.
I relief grind at a very low angle, as taught by John Juranitch, so there is little or no shoulder on or near my knife edges, except for a small low angle microbevel. This being so, maybe my thin flat edges and thin convex edges are so similar that there is little or no real-world difference in how they actually perform.
What helped me to understand convexity better was when I read that, since it's impossible to repeatedly hold the exact same angle when freehand sharpening, some convexity will naturally occur. You described a similar process, with a similar result, very well and clearly in your second paragraph.
After reading your explanation, I re-read this quotation with much more understanding than the first time. This one sentence pretty much says it all, if I understand it correctly, and I think I do now.
It doesn't require mathematical modelling at all. The way in which we calculate the edge angle - and you can call it "effective" or any other term you choose - is as follows: Choose a measured distance behind the apex along the bevel (W) and measure (pinch-micrometer), and also measure the thickness of the bevel at that distance, then do basic trig:Yeah, it's technically possible to measure the angle of the intersection of two arcs, but it requires mathematically modeling those arcs first, which is kind of a pain in the butt, making it impractical for all but theoretical purposes in this context.
From a practical perspective, you can use a hard material (that's softer than steel) such as plexiglass, to find the effective angle by laying the blade flat on the surface of the material, and slowly tilting the spine up until a forward push on the blade causes it to bite. The reason to use a hard material as the test medium is to reduce how much the material will deflect under pressure (which should be kept light in any case with this test) so you get a closer result to the actual edge angle. Since an edge will only bite at any angle greater than the bevel angle, you can find the angle by approximating just the tiniest bit under the angle at which the edge will actually bite.
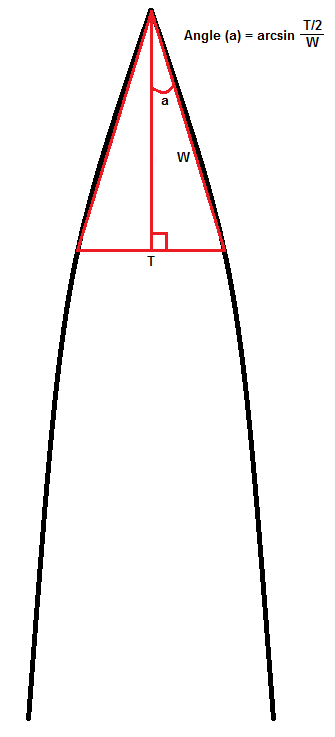
The theoretical angle of intersection between two mathematically modeled curves (that do not exist in reality) is defined as the angle of intersection of the tangents of each curve applicable at only that single point of intersection which bears no relation to a knife bevel whatsoever, which is one reason why it isn't actually done (and FortyTwo is correct that it is also physically impossible since we do not measure curved lines, only straight ones). The fact is, even the math to attain the tangent of a curve is based on taking the secant lines from beneath the convex curve to smaller and small lengths (to a limit). The angle of the convex bevel is defined by the angle of smallest measurable secant lines beneath that curve (W above). In other words, the angle of a convex edge is derived from the angle of the corresponding FLAT grind beneath it, which is necessarily that little bit thinner. That is the angle of your convex edge.
Besides that, FortyTwoBlades' recommendation of just using the edge and seeing what angle it cuts like is perfect
 If it seems to be cutting at too high of an angle, you may have rounded the edge over or have a burr bent the other way, while if it seems to cut at too shallow of an angle then you may have a burr bent toward the medium being cut.
If it seems to be cutting at too high of an angle, you may have rounded the edge over or have a burr bent the other way, while if it seems to cut at too shallow of an angle then you may have a burr bent toward the medium being cut.Here is an image of how CATRA measures edge-angle if you can take a cross-section of the edge, which you won't do, hence my recommendation to measure the bevel width (you can also find examples of this described in patents filed by companies such as Gillette for their razor blades). Another great resource for stuff like this is the blog https://scienceofsharp.com/ - amazing sets of blade apex SEM