Cushing H.
Gold Member
- Joined
- Jun 3, 2019
- Messages
- 2,714
Given what I just posted, lets play with the value of Kp a little:
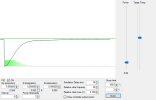
Keeping everything the same, but setting Kp = 0.5 – we would expect that the rise to temperature is faster, and that the offset is smaller: (and that is exactly what you see happen).
Unfortunately, you can continue to make Kp larger and reduce the offset, but only to a point. In this case, when Kp = 1.0, things look good:
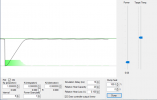
(by the way, if you look at the bars on the bottom of the screenshots above, you can see how the proportional band becomes smaller and smaller by way of how fast the height of the bars (controller ouput) drops off faster as Kp gets bigger.)
BUT, at Kp=10, the oven temperature is rising so fast, and the heating element shuts off so close to the setpoint that it can not shed its residual heat fast enough – and you get an overshoot of temperature (and you start getting an oscillation above and below the set point):
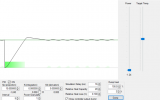
This is NOT a good place to be. I have an understandable example, I think, to justify the following statement – but for now I will just state it: You ALWAYS want to be operating in the proportional band, because it is within that band that the controller has the ability to “correct” the current situation (it can increase or decrease power to the heating elements somewhat). Outside of the proportional band (i.e. above the setpoint), it has no such power (the elements are already off, and unless you have cooling built into the oven controlled by another PID, you have no control over the situation.
Oscillations like the above are “unstable” and not controllable – AND when you add additional controls like the integral term (which is really sensitive), things can get really unstable really fast.
So – to close out this part, I will make the following recommendation:
Try first “tuning” your PID by turning off both integral and differential terms. Then set the proportional band (see below re. actual controllers) to a very very wide value. Fire the thing up, and see where you land in terms of temperature rise time and offset. Then continue making the proportional band smaller and smaller until you JUST see an overshot like the one above. THEN back off to the last value of Kp that did not give you an overshot, and take note of the offset. Then increase the setpoint higher by the the value of the offset – and you should then have an oven that settles in pretty cleanly at the temperature you want it to be at.
(if you can not get it to do this, then you have some really bad mis-match in the system – like a really, really strong heating element and a huge amount of insulation (this situation looks like this:
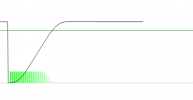
Or really bad insulation, and the heating element just can not put enough heat into the oven to overcome the loss, which looks like this:

Unfortunately, different controllers implement slightly the algorithm in slightly different ways. The Inkbird ITC-106 calls for you to specify a proportional band in the range of 0-9999. It does not give units, so Sitting here, I have no idea if that is degrees, or is actually meant to be the value of Kp (which does not have units and can effectively take on any value). If it is degrees (as in it is implicitly using the equation Proportional band (in degrees) = 100/Kp, then setting this to a larger value should increase the proportional band. However, if it is actually meant to be the value of Kp itself, then (as in the above discussion) setting it to a larger value will decrease the proportional band. Like I said, the Inkbird manual is pretty bad. Hopefully someone out there can clarify the behavior they see with their Inkbird?
On the other hand, the Auber SYL-2362A2 has a nice understandable manual (but you need to do a little math). For the proportional band, it has you input the actual band (temperature range) you want, but as a percentage of the control range (which is defined by the thermocouple type). The example they give is that for a K-type thermocouple, which controls up to 1500C, if you set this value to 5 (i.e. 5%), then the proportional band is 1500 * 5 = 75 degrees C.
ON the other hand – once you understand how your controller uses this input parameter, all you need to do is somewhat arbitrarily adjust the parameter up (or down) to alter the proportional band until you get the response you want……
Keeping everything the same, but setting Kp = 0.5 – we would expect that the rise to temperature is faster, and that the offset is smaller: (and that is exactly what you see happen).

Unfortunately, you can continue to make Kp larger and reduce the offset, but only to a point. In this case, when Kp = 1.0, things look good:

(by the way, if you look at the bars on the bottom of the screenshots above, you can see how the proportional band becomes smaller and smaller by way of how fast the height of the bars (controller ouput) drops off faster as Kp gets bigger.)
BUT, at Kp=10, the oven temperature is rising so fast, and the heating element shuts off so close to the setpoint that it can not shed its residual heat fast enough – and you get an overshoot of temperature (and you start getting an oscillation above and below the set point):

This is NOT a good place to be. I have an understandable example, I think, to justify the following statement – but for now I will just state it: You ALWAYS want to be operating in the proportional band, because it is within that band that the controller has the ability to “correct” the current situation (it can increase or decrease power to the heating elements somewhat). Outside of the proportional band (i.e. above the setpoint), it has no such power (the elements are already off, and unless you have cooling built into the oven controlled by another PID, you have no control over the situation.
Oscillations like the above are “unstable” and not controllable – AND when you add additional controls like the integral term (which is really sensitive), things can get really unstable really fast.
So – to close out this part, I will make the following recommendation:
Try first “tuning” your PID by turning off both integral and differential terms. Then set the proportional band (see below re. actual controllers) to a very very wide value. Fire the thing up, and see where you land in terms of temperature rise time and offset. Then continue making the proportional band smaller and smaller until you JUST see an overshot like the one above. THEN back off to the last value of Kp that did not give you an overshot, and take note of the offset. Then increase the setpoint higher by the the value of the offset – and you should then have an oven that settles in pretty cleanly at the temperature you want it to be at.
(if you can not get it to do this, then you have some really bad mis-match in the system – like a really, really strong heating element and a huge amount of insulation (this situation looks like this:

Or really bad insulation, and the heating element just can not put enough heat into the oven to overcome the loss, which looks like this:

Unfortunately, different controllers implement slightly the algorithm in slightly different ways. The Inkbird ITC-106 calls for you to specify a proportional band in the range of 0-9999. It does not give units, so Sitting here, I have no idea if that is degrees, or is actually meant to be the value of Kp (which does not have units and can effectively take on any value). If it is degrees (as in it is implicitly using the equation Proportional band (in degrees) = 100/Kp, then setting this to a larger value should increase the proportional band. However, if it is actually meant to be the value of Kp itself, then (as in the above discussion) setting it to a larger value will decrease the proportional band. Like I said, the Inkbird manual is pretty bad. Hopefully someone out there can clarify the behavior they see with their Inkbird?
On the other hand, the Auber SYL-2362A2 has a nice understandable manual (but you need to do a little math). For the proportional band, it has you input the actual band (temperature range) you want, but as a percentage of the control range (which is defined by the thermocouple type). The example they give is that for a K-type thermocouple, which controls up to 1500C, if you set this value to 5 (i.e. 5%), then the proportional band is 1500 * 5 = 75 degrees C.
ON the other hand – once you understand how your controller uses this input parameter, all you need to do is somewhat arbitrarily adjust the parameter up (or down) to alter the proportional band until you get the response you want……

